Game of Genomes: Part 1
Architecture and Recombination Dynamics of a Dooder's Genetic Neural Network
This is the first of two articles exploring the architecture of the Dooder’s genetic neural network, along with the methodologies employed for recombination during the process of reproduction. Take a look at the Experiment List to see previous articles. For a complete overview of the project or to see the code go to GitHub repository.
Blueprint to Behavior
I have been brainstorming ways to design a system that replicates mechanisms common in natural organisms. While the argument of Nurture vs Nature may be a matter of ongoing debate, ample evidence suggests behavior is heavily influenced by genetic predispositions and environmental conditions. Genes act as immutable boundaries on behavior, yet provide a structure enabling an organism to adapt to existing conditions (Genotype vs Phenotype).
A genotype refers to the genetic makeup of an organism - the set of genes that it carries. It's like the blueprint or the hard-coded constraints, which determines the potential features an organism could have. On the other hand, a phenotype is the visible or observable characteristics of that organism, which are a result of the interaction between the organism's genotype and the environment. In essence, the genotype sets the potential range of traits an individual may have, but the phenotype is the actual manifestation of those traits, often influenced and modified by environmental factors.
I aim to utilize the concepts of genotype and phenotype as a framework to model Dooder's behavior. These interconnected models are embedded within the neural network's structure, governing how a Dooder behaves. In a previous article, I discussed the functionality of the energy-seeking gene, and now I intend to explore the specifics of the neural network architecture itself.
In neural networks, the magic truly unfolds in the hidden layers. These layers function as the computational engine, where the input data is transformed through various mathematical operations determined by the weights and biases of the neurons within these layers. Each layer takes the output from the previous one, applies its unique transformation, and passes the result onto the next. As the data moves through each layer, the network identifies and abstracts increasingly complex features, leading to a final output that can make accurate predictions or decisions.
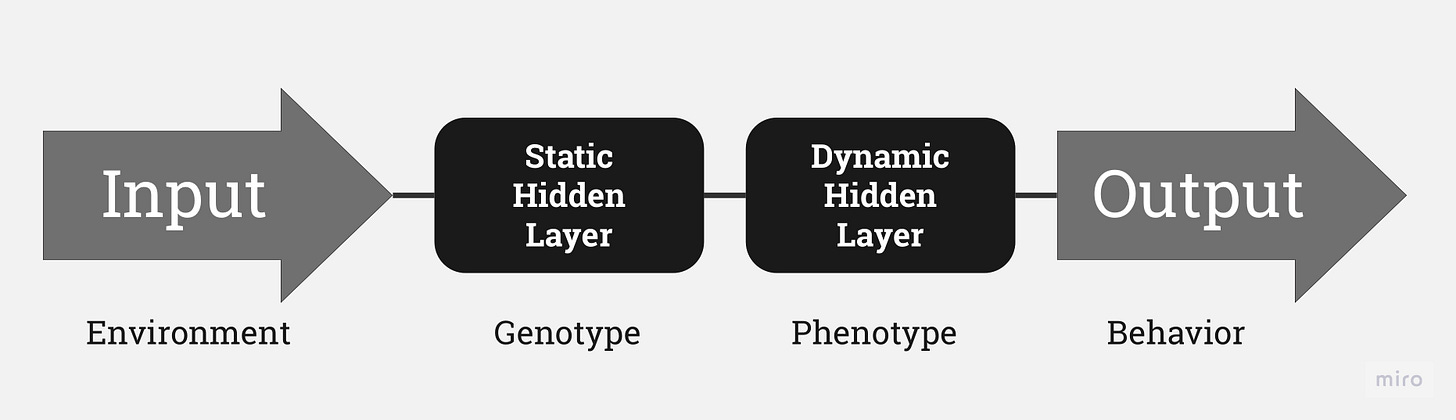
Static Hidden Layer (Genotype)
Inherited
Does not change during a Dooder’s lifespan
Evolves slowly (generation over generation)
The static layer is frozen within a Dooder's internal models, remaining fixed throughout its duration. This design draws inspiration from transfer learning, a widely used technique in machine learning. Transfer learning involves inheriting pre-trained models and fine-tuning them for specific tasks, a strategy increasingly employed with Large Language Models (LLMs).
A user can leverage a pre-trained model as a foundation for their particular use case. By adding supplementary hidden layers, the model becomes adaptable to unique scenarios without having to undergo extensive training. Basically, a new model can inherit the learned features from the pre-trained model.
In my use case, the static layer starts as an untrained element, essentially random noise. This layer evolves over generations, as the simulation's selection pressure filters out Dooders that fail to survive. Future generations inherit this better fitting genetic foundation.
Dynamic Hidden Layer (Phenotype)
Inherited
Adapts to the Dooder’s experience
Evolves quickly (cycle over cycle)
Unlike the static layer, the dynamic layer is malleable and continuously revises itself after each cycle the Dooder interacts in the simulation. This property enables the dynamic layer to engage in learning processes and adaptation, through back-propagation.
This dynamic layer is passed down, much like genetic information in natural organisms. It carries information about the patterns and strategies that have proven successful in the past. However, this layer's uniqueness lies in its capacity for flexibility and adaptation. It incorporates the Dooder's experiences, altering its function based on the lessons learned from each simulation cycle.
Over time, these adaptations contribute to the Dooder's ability to survive and thrive in the environment it operates in. This process is akin to an organism's phenotype adapting to its surroundings, improving its chances of survival.
In this model, the genetic (static) layer sets the groundwork, while the dynamic layer captures the Dooder's experiences and learnings. I hope that the integration of both layers is what creates a complex, adaptive system that mirrors the inherent adaptability and resilience of natural organisms.
The Birds and the Biases
To emulate the process of reproduction found in nature, I will experiment with recombination techniques to create new generations of Dooders from two parent genetic neural networks. The first recombination techniques I will experiment with are: Crossover, Lottery, Averaging, and Random Range.
Crossover
Inspired by the genetic recombination process seen in nature, this technique selects a random crossover point within the layer weights of the two parent Dooders. We then construct the offspring's layer weights by combining the weights from parent #1 to the left of the crossover point and the weights from parent #2 to the right of the crossover point. This mimics the genetic shuffling observed during sexual reproduction, introducing variation into the offspring population.
# With a random crossover point of 3
parent_1 = [.1, .2, .3, .4, .5]
parent_2 = [.6, .7, .8, .9, .1]
offspring = [.1, .2, .3, .9, .1]Lottery
The offspring's weights are determined by a simple lottery system. Each weight is chosen randomly from either parent #1 or parent #2. This method introduces an additional element of randomness into the generation of the next set of Dooders, possibly enhancing the chances of discovering novel and potentially beneficial configurations of weights.
parent_1 = [.1, .2, .3, .4, .5]
parent_2 = [.6, .7, .8, .9, .1]
offspring = [.1, .2, .8, .9, .5]Averaging
The averaging methodology takes a more conservative route to recombination. Rather than leaning heavily on either parent, this approach generates the offspring's weights by taking the average of corresponding weights from parent #1 and parent #2. This method may result in a smoother transition from one generation to the next, encouraging the incremental refinement of successful weight configurations while still introducing some degree of variation.
parent_1 = [.1, .2, .3, .4, .5]
parent_2 = [.6, .7, .8, .9, .1]
offspring = [.35, .45, .55, .65, .30]Random Range
Lastly, the random range method operates on a principle of random selection within established limits. Here, each weight for the offspring is chosen as a random value that falls within the range of the corresponding weights of parent #1 and parent #2. This approach maintains the extent of variation exhibited by the parents, but allows for the offspring to explore unique weight combinations that might not have been present in either parent.
parent_1 = [.1, .2, .3, .4, .5]
parent_2 = [.6, .7, .8, .9, .1]
offspring = [.23, .28, .71, .53, .45]It is important to note that none of these techniques involve mutation, an essential role in nature that introduces random changes in an organism's genetic sequence. This absence of mutation means that these methods are primarily reshuffling and recombining existing genetic material, without introducing entirely new genetic variations. Each of these recombination methodologies carries its own advantages and disadvantages and encourages different rates and types of evolutionary change that I aim to explore.
Next up
In part two, I will leverage genetic programming to experiment with the various recombination techniques through Recursive Artificial Selection (RAS). This approach involves identifying the most fit agents from a set of simulations and utilizing them as the genetic pool for the subsequent generation, effectively simulating natural selection with a more deliberate and time-efficient approach. The goal is to see how the recombination techniques evolve the genetic pool over multiple generations of Dooders.

